Geometría y medida
Resumen del Cuestionario
0 of 61 Preguntas completed
Preguntas:
Información
Ya has completado el cuestionario anteriormente. Por lo tanto no puedes iniciarlo de nuevo.
Cargando Cuestionario…
Debes iniciar sesión o registrarte para empezar el cuestionario.
En primer lugar debes completar esto:
Resultados
Resultados
0 de 61 Preguntas respondidas correctamente
Tu tiempo:
El tiempo ha pasado
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categorías
- Sin categorizar 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- Actual
- Revisar
- Respondido/a
- Correcto
- Incorrecto
- Pregunta 1 de 61
1. Pregunta
Un barco M sale del punto A(−1;−2)A(-1;-2) hacia el punto B(5;yb)B(5;yb) y se desplaza √52√52 al noreste. Otro barco N ubicado en C(6;yc)C(6;yc) se dirige hacia el sureste al punto D(−2;6)D(-2;6), desplazándose √208√208. Se podría decir que sus trayectorias forman rectas:
CorrectoIncorrecto - Pregunta 2 de 61
2. Pregunta
Relaciona cada vector con sus coordenadas del origen y extremo. Vector Coordenadas A (origen) y B (extremo) 1. \(\overrightarrow {AB} = – 8\vec i + 5\vec j\) a) A(2;-3) y B(-3;5) 2. \(\overrightarrow {AB} = 5\vec i – 8\vec j\) b) A(-3;5) y B(2;-3) 3. \(\overrightarrow {AB} = 8\vec i – 5\vec j\) c) A(5;-3) y B(-3;2) d) A(-3;2) y B(5;-3)
CorrectoIncorrecto - Pregunta 3 de 61
3. Pregunta
Selecciona las coordenadas del extremo B del vector
CorrectoIncorrecto - Pregunta 4 de 61
4. Pregunta
Los automóviles A, B, C y D se mueven de acuerdo a los vectores mostrados. ¿Cuál de los 4 automóviles ha recorrido mayor distancia?
CorrectoIncorrecto - Pregunta 5 de 61
5. Pregunta
La siguiente tabla muestra las trayectorias seguidas por el desplazamiento de 4 móviles de acuerdo con los vectores especificados. Determina qué trayectorias son perpendiculares. Móvil Vector A \(3\vec i – \vec j\) B \( – \vec i + 3\vec j\) C \(2\vec i + 6\left( j \right)\) D \( – 3\vec i + \vec j\)
CorrectoIncorrecto - Pregunta 6 de 61
6. Pregunta
Determina un vector de magnitud 8, paralelo a \(8\vec i – 6\vec j\)
CorrectoIncorrecto - Pregunta 7 de 61
7. Pregunta
Determina la expresión de un vector de módulo 10 y opuesto al mostrado en la gráfica.
CorrectoIncorrecto - Pregunta 8 de 61
8. Pregunta
Una torre en estructura metálica para la transmisión de energía está sometida a las fuerzas, en Newtons, que se indican en la figura, donde cada cuadrícula corresponde a 10N. Determine la fuerza F6 que debería adicionarse para que la estructura esté en equilibrio (sumatoria de fuerzas igual a cero) ya que los elementos requieren estabilidad.
CorrectoIncorrecto - Pregunta 9 de 61
9. Pregunta
Un astrólogo se encuentra analizando el comportamiento de la velocidad del plasma de una estrella a 23 años luz. Debe encontrar la velocidad promedio del plasma para lo cual cuenta con la siguiente gráfica que muestra la velocidad del plasma en la parte frontal de la esfera. Determinar la velocidad del plasma de la estrella que resulta de sumar las corrientes individuales del lado frontal de la estrella \(\vec u + \vec v + \vec w\) y restar el promedio de su lado posterior que tiene una velocidad de plasma promedio de \( – 5\vec i – 6\vec j\).
CorrectoIncorrecto - Pregunta 10 de 61
10. Pregunta
Selecciona la representación retangular del vector de la gráfica.
CorrectoIncorrecto - Pregunta 11 de 61
11. Pregunta
Un objeto está atado a dos cuerdas por dos extremos opuestos. Dos niños A y B compiten por ganar el objeto halando ambos a la vez en sentido contrario. La fuerza de A está representada por el vector \(\overrightarrow {{F_A}} = – 50\vec i + 0\vec j\)y la de B mide 55N. Entonces se puede afirmar que:
CorrectoIncorrecto - Pregunta 12 de 61
12. Pregunta
Dos vehículos A y B se mueven con aceleración constante. El vehículo B tiene una velocidad inicial \[{V_o}B = \left( {50\vec i – 4\vec j} \right)\frac{{km}}{h}\], y después de 2 horas alcanza una velocidad final \[{V_f}B = \left( {54\vec i – 16\vec j} \right)\frac{{km}}{h}\]. Si se conoce que la aceleración del vehículo A es el doble que la aceleración del vehículo B, determine la aceleración del vehículo A, en \[\frac{{km}}{{{h^2}}}\], para calcular a qué hora llegará a su destino.
CorrectoIncorrecto - Pregunta 13 de 61
13. Pregunta
Los automóviles A y B ejercen una fuerza de tensión sobre la carga de acuerdo a las magnitudes y direcciones del gráfico. Si la carga se mueve verticalmente en el eje Y, ¿cuál es el ángulo Z en el que se direcciona el automóvil B?
CorrectoIncorrecto - Pregunta 14 de 61
14. Pregunta
Dados los vectores del siguiente gráfico determina la operación: \(\vec a – \vec b\)
CorrectoIncorrecto - Pregunta 15 de 61
15. Pregunta
El movimiento de un móvil A se representa por un vector \({\vec a}\) de magnitud 2√2 km y forma un ángulo de 45° en sentido antihorario con el eje Y positivo; y el movimiento de un móvil B, representado por un vector \({\vec b}\), tiene como posición inicial el punto (4,0) km y posición final (8,-3) km. Determinar el valor de la operación: \(\vec a – 2\vec b\)
CorrectoIncorrecto - Pregunta 16 de 61
16. Pregunta
Un bote posee cuatro turbinas que, debido al uso, están desalineadas. Por ello, cada una de las dos primeras turbinas le proporciona al bote una velocidad representada por el vector A, la tercera turbina proporciona la velocidad que representa el vector C y la cuarta turbina la velocidad del vector -B, todo en m/s . Si un pescador necesita obtener la velocidad total del bote para poder conocer hacia dónde debe marcar el rumbo para realizar la pesca del día, determine el vector.
CorrectoIncorrecto - Pregunta 17 de 61
17. Pregunta
Al golpear una bola de billar, esta describe una trayectoria dada por el vector \(\vec B = 40cm,NE\). Choca contra el límite de la mesa, rebota y describe una trayectoria dada por el vector \[\vec C = 18cm,330\]. ¿Cuál de las opciones describe el vector que se forma entre el punto de partida y el punto de llegada?
CorrectoIncorrecto - Pregunta 18 de 61
18. Pregunta
Los siguientes vectores nos indican 3 desplazamientos hechos por una persona mientras daba un paseo en el parque. \(\vec A = \left( { – 2\surd 2, – 2\surd 2} \right)m\) \(\vec B = \)=B→=24m; O, 45˚ del N \(\vec C = \left( {8\surd 2\vec i – 2\surd 2\vec j} \right)m\) Si después de 10 minutos de caminata se detiene a descansar en una banca, ¿cuánto deberá recorrer desde la banca al lugar exacto desde el que partió?
CorrectoIncorrecto - Pregunta 19 de 61
19. Pregunta
Un estudiante de la especialización de Informática ha desarrollado una aplicación para dispositivos móviles que puede determinar la distancia y los desplazamientos realizados, siempre y cuando se disponga de conexión GPS. El estudiante quiere comprobar si la aplicación está funcionando correctamente por lo que ha encendido la aplicación al salir de la casa y realiza distintos desplazamientos hasta llegar a la institución donde estudia. Al avanzar hacia su destino, en su aplicación se registra el primer desplazamiento de (8;6) km; al llegar a una intersección toma un nuevo rumbo de (6:8) km con respecto a la intersección; y, finalmente se registra un desplazamiento de (-8,-6) km hasta llegar a la institución. Si la aplicación funciona correctamente, ¿cuál sería el desplazamiento neto, en km, que debe mostrar?
CorrectoIncorrecto - Pregunta 20 de 61
20. Pregunta
Con base en el gráfico que muestra la posición de dos barcos, respecto a los observadores en A (2,2) para el vector \({\vec u}\) y C (-2,-2) para el vector \({\vec v}\). Determinar el vector \(\vec u + 3\vec v\) correspondiente al desplazamiento que realizará el barco \({\vec u}\) con respecto al barco \({\vec v}\) cuando este último triplique su desplazamiento.
CorrectoIncorrecto - Pregunta 21 de 61
21. Pregunta
Dos vectores que tienen origen común están dados por: \(\vec A\left( {\frac{1}{5};21} \right)\) y \(\vec B\left( {35; – \frac{1}{3}} \right)\). ¿Cuál es el ángulo comprendido entre ellos?
CorrectoIncorrecto - Pregunta 22 de 61
22. Pregunta
Dos barcos salen del mismo puerto con rumbos diferentes. El barco A parte en dirección N60˚E a una velocidad de 15 km/h, y el barco B va con rumbo NO con una velocidad de 20 km/h. Si se supone que ambos siguieron su rumbo en línea recta, ¿cuál será la posición relativa del barco B con respecto al A, luego de 5 horas de navegación?
CorrectoIncorrecto - Pregunta 23 de 61
23. Pregunta
¿Qué distancia se desplazó un objeto que inicialmente se encontraba en las coordenadas A(-7,11) y llegó a las coordenadas B(13; -4)?
CorrectoIncorrecto - Pregunta 24 de 61
24. Pregunta
Dos edificios se encuentran juntos tal como se muestra en la figura. La terraza del edificio A está a 21 metros del piso, y la del edificio B, a 12 metros. Una persona que se encuentra en el punto M, define los vectores posición de las terrazas de cada edificio según los ángulos mostrados. ¿Cuál será la posición relativa de la terraza de A con respecto a B?
CorrectoIncorrecto - Pregunta 25 de 61
25. Pregunta
En una mesa de billar hay dos bolas A y B en reposo, una al lado de la otra. Después del impulso, la bola A se desplaza con una aceleración de 12 \(\frac{{cm}}{{{s^2}}}\) y la bola B con una aceleración de 24 \(\frac{{cm}}{{{s^2}}}\). Si el ángulo formado entre ambas bolas es de 60°, ¿cuál será la distancia, en cm, entre las dos bolas después de un segundo, considerando que ninguna de ellas ha caído en el hoyo?
CorrectoIncorrecto - Pregunta 26 de 61
26. Pregunta
Dos personas se encuentran en un campo irregular y para evitar que los objetos frágiles que llevan consigo se rompan, los transportan en una caja que deben arrastrar de manera horizontal. ¿Con qué ángulo deben halar la caja para que siga esta trayectoria? Considere los datos del gráfico:
CorrectoIncorrecto - Pregunta 27 de 61
27. Pregunta
Las personas A y B se mueven de acuerdo a los vectores dados mientras que la persona C se queda inmóvil. ¿Cuál de las personas que se movieron estará más cerca a la persona inmóvil al terminar su desplazamiento?
CorrectoIncorrecto - Pregunta 28 de 61
28. Pregunta
La persona A y la persona B se mueven de acuerdo a los vectores mostrados en la figura. ¿Cuál es la posición final de B con respecto a la posición final de A?
CorrectoIncorrecto - Pregunta 29 de 61
29. Pregunta
Con base en el gráfico que muestra la posición de dos barcos, respecto a los observadores en (1;1) para \({\vec a}\) y (-2;-1) para \({\vec b}\). Determine el vector \( – 3\vec a + \vec b\) correspondiente al desplazamiento que realizará el barco cuando \({\vec a}\) cambie su dirección y triplique su desplazamiento con respecto al barco \({\vec b}\).
CorrectoIncorrecto - Pregunta 30 de 61
30. Pregunta
Juan camina en el parque, y llega al punto (15,-3) km. Si su posición inicial se representa por el vector \(\left( {3\vec i + \vec j} \right)km\) km. Determina en km el vector que indica su desplazamiento.
CorrectoIncorrecto - Pregunta 31 de 61
31. Pregunta
¿Cuál de las siguientes curvas corresponde con la ecuación \({y^2} = – 8x\) *imagen*
CorrectoIncorrecto - Pregunta 32 de 61
32. Pregunta
¿Cuál es el foco correspondiente a la siguiente parábola? \({x^2} + y = 9\)
CorrectoIncorrecto - Pregunta 33 de 61
33. Pregunta
¿Qué ecuación corresponde con la directriz de la siguiente parábola? \({\left( {y – 2} \right)^2} = 20x + 2\)
CorrectoIncorrecto - Pregunta 34 de 61
34. Pregunta
Se tiene una parábola cuyo foco es F(1/8 , 2) y su directriz corresponde con la recta y = 15/8. Cuál es la ecuación de la parábola?
CorrectoIncorrecto - Pregunta 35 de 61
35. Pregunta
¿Cuál es el vértice de una parábola cuya directriz sea la recta x=7/24 y su foco sea (5/8 , 1/6)?
CorrectoIncorrecto - Pregunta 36 de 61
36. Pregunta
¿Cuál es la ecuación de la directriz de la siguiente parábola? \({x^2} – 2x = y + 8\)
CorrectoIncorrecto - Pregunta 37 de 61
37. Pregunta
¿Hacia dónde se extiende la siguiente parábola? \({y^2} – 24 = 4x\)
CorrectoIncorrecto - Pregunta 38 de 61
38. Pregunta
Se tiene la siguiente parábola: \(2{x^2} + 5x = 9y – 1\) El punto (-5/4 , -49/36) representa:
CorrectoIncorrecto - Pregunta 39 de 61
39. Pregunta
¿Con qué ecuación corresponde la siguiente curva? *imagen*
CorrectoIncorrecto - Pregunta 40 de 61
40. Pregunta
Dada la ecuación de la hipérbola, identifique el valor de su excentricidad. \(144{x^2} – 36{y^2} – 5184 = 0\)
CorrectoIncorrecto - Pregunta 41 de 61
41. Pregunta
Identifique la forma canónica de la ecuación. \({x^2} – 8x + {y^2} – 16y + 16 = 0\)
CorrectoIncorrecto - Pregunta 42 de 61
42. Pregunta
Dada la ecuación de la circunferencia, calcule su centro y su radio. \({x^2} + {y^2} + 2x – 2y – 2 = 0\)
CorrectoIncorrecto - Pregunta 43 de 61
43. Pregunta
Relacione el tipo de cónica con su ecuación general. Tipo Ecuación 1. Circunferencia a) \(9{x^2} – 16{y^2} – 108x + 128y + 212 = 0\) 2. Parábola b) \({x^2} + {y^2} – 4x + 10y + 13 = 0\) 3. Elipse c) \({x^2} + 4{y^2} – 6x – 16y + 21 = 0\) 4. Hipérbola d) \({y^2} – 8x + 6y + 1 = 0\)
CorrectoIncorrecto - Pregunta 44 de 61
44. Pregunta
La plusvalía de un terreno depende de la localización del mismo. Si los terrenos se encuentran ubicados en las coordenadas de la siguiente gráfica, y la plusvalía está definida por la siguiente función \[P\left( {x,y} \right) = {x^2} + {y^2}\] Determinar el terreno que obtendría la mayor plusvalía.
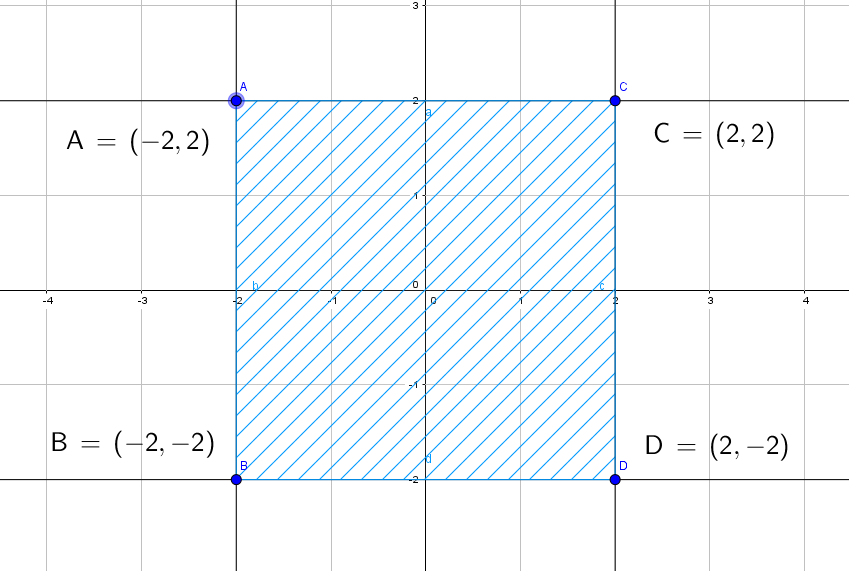 CorrectoIncorrecto
CorrectoIncorrecto - Pregunta 45 de 61
45. Pregunta
El gráfico que se muestra a continuación representa los posibles métodos de producción de x laptops HP y y laptops Toshiba, en relación con el número de laptops defectuosas en la producción. La función que define el número de laptops defectuosas está dada por la siguiente expresión \(T\left( {x,y} \right) = 5x – y + 1\) Determinar el máximo número de laptops defectuosas.
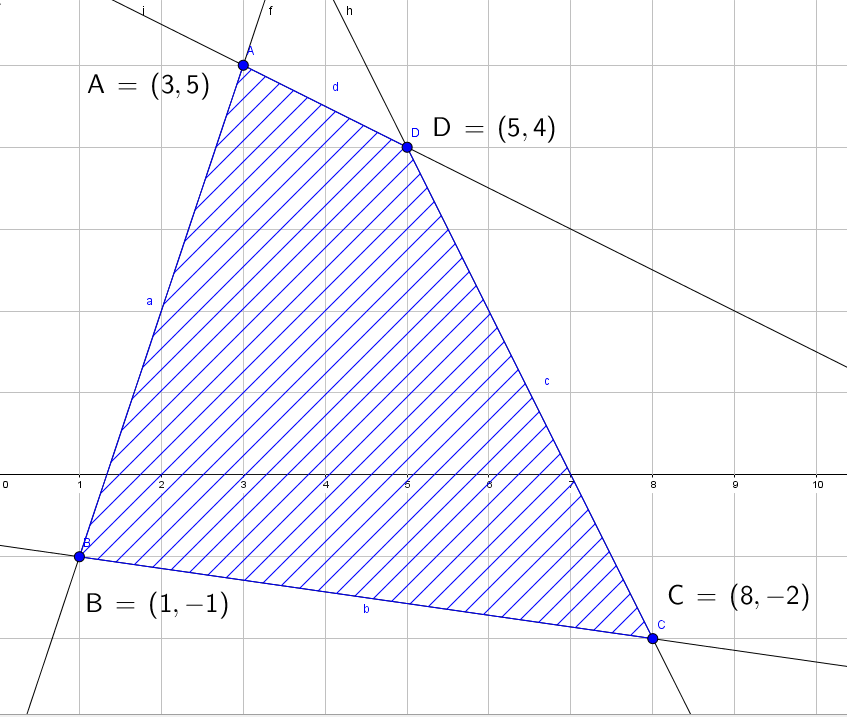 CorrectoIncorrecto
CorrectoIncorrecto - Pregunta 46 de 61
46. Pregunta
La plusvalía de un terreno depende de la localización del mismo, si los terrenos se encuentran ubicados en las coordenadas de la siguiente gráfica, y la plusvalía está definida por la siguiente función \(P\left( {x,y} \right) = {x^2} + y + 2\) Si Juan quiere decidir que terreno debe comprar, determine cuál es la opción correcta.
CorrectoIncorrecto - Pregunta 47 de 61
47. Pregunta
Un submarino debe decidir qué lugares puede explorar dependiendo de la profundidad y temperatura, sabiendo que la expresión que determina la presión dentro del submarino está dada por \(P\left( {x,y} \right) = 3x – 3y + 10\)
CorrectoIncorrecto - Pregunta 48 de 61
48. Pregunta
Un avión debe decidir qué lugares puede volar dependiendo de la velocidad y temperatura del viento, sabiendo que la expresión que determina la presión dentro del submarino está dada por \(P\left( {x,y} \right) = x – y + 3\) sí x es la velocidad del viento y y la temperatura de viento. Según la siguiente gráfica determinar los puntos que destruirían el avión si la máxima presión que soporta el submarino es 10 psi.
CorrectoIncorrecto - Pregunta 49 de 61
49. Pregunta
Una ambulancia debe llegar al hospital más cercano, para ello debe tomar en cuenta las siguientes rutas, la ruta A, B y C presentan las siguientes condiciones expresadas en el siguiente gráfico con respecto a la densidad de tráfico x y cantidad de semáforos y, sabiendo que la función que define el tiempo en el cual llegará al hospital más cercano es la siguiente \(t\left( {x,y} \right) = x – 2y + 4\) Encuentre la mejor ruta para salvar al paciente.
CorrectoIncorrecto - Pregunta 50 de 61
50. Pregunta
El consumo de luz eléctrica de una fábrica está determinado por un motor y un horno eléctrico, sí el motor y el horno pasan encendidos x y y horas diarias determinar el número óptimo de horas que debe utilizar cada equipo, para obtener el menor consumo eléctrico. La función que determina el consumo eléctrico está dada por la expresión \(E\left( {x,y} \right) = {x^2} + y + 13\)
CorrectoIncorrecto - Pregunta 51 de 61
51. Pregunta
Un panadero dispone de 10000 kg de harina. En la elaboración de dos tipos diferentes de pan, A y B, utiliza 2 kg en la docena del tipo A y 3,5 kg en la docena del tipo B. Se demora 2 horas elaborando la docena del primero y una en la docena del segundo. Dispone de 6 horas de trabajo. La docena del pan A cuesta $1,20 y la del pan B, $1,68 ¿Determina la función objetivo y las restricciones que permitan obtener el máximo beneficio?
CorrectoIncorrecto - Pregunta 52 de 61
52. Pregunta
Una señora vende dos tipos de torta, T1 y T2. La elaboración de ambas requiere de dos tipos de batidas, una con paleta y otra con batidora; la batida con paleta para T1 dura 1/3 de hora mientras que para T2, media hora; la batida con batidora para T1 requiere el mismo tiempo que con paleta y para T2, 1/6 de hora. Disponiendo por semana de 100 horas para el batido con paleta y de 80 horas para el batido con batidora, y sabiendo que cada unidad de T2 tiene una ganancia de 2/3 de la ganancia de T1, se desea planificar la producción de manera que se obtenga un beneficio óptimo. Selecciona el gráfico que representa la zona factible para la solución de este problema.
CorrectoIncorrecto - Pregunta 53 de 61
53. Pregunta
La tabla muestra las horas que por unidad requiere la elaboración de dos modelos diferentes de pantalones en un taller de costura. Cada pantalón pasa por las tres máquinas en el mismo orden. ¿Cuál es la función objetivo que permite maximizar el beneficio?
CorrectoIncorrecto - Pregunta 54 de 61
54. Pregunta
Una persona compró cierto número de libros por $1 800. Si compra 6 libros menos por el mismo dinero, cada uno le cuesta $10 más. ¿Cuánto le costó cada libro?
CorrectoIncorrecto - Pregunta 55 de 61
55. Pregunta
Relaciona la solución del sistema de inecuaciones con su representación gráfica.
CorrectoIncorrecto - Pregunta 56 de 61
56. Pregunta
Yolanda diseña dos modelos de cartera con cuero torcido de color morado y verde. Para el primer diseño utiliza un metro de cada color, para el segundo 5/4 de metro del color morado y 8/9 de metro de verde. Al hacer el inventario determinó que cuenta con 15 metros de color morado y más de 16 metros del verde. Si por cada modelo de cartera obtiene la misma utilidad, pero ella anhela maximizar la producción de manera que se obtenga el máximo beneficio bajo las condiciones actuales, entonces se puede determinar que:
CorrectoIncorrecto - Pregunta 57 de 61
57. Pregunta
Un levantador de pesas consume dos componentes 1 y 2 con el fin de suplir las vitaminas A y B que su cuerpo necesita diariamente. La tabla muestra el requerimiento de consumo mínimo diario en gramos de proteínas A y B para estos deportistas, el aporte que contienen los componentes 1 y 2 y el precio por kg de cada componente. Con base en lo anterior, ¿cuáles son las restricciones sobre el número de componentes que se deben consumir diariamente, manteniendo la mínima dieta y ahorrando al máximo?
CorrectoIncorrecto - Pregunta 58 de 61
58. Pregunta
Con 600 g de harina se elaboran empanadas grandes y pequeñas. Las grandes pesan 40 g y las pequeñas 30 g. Se necesitan al menos tres grandes, y al menos el doble de pequeñas que de las grandes. Cada empanada grande proporciona un beneficio de 2 centavos y la pequeña 1 centavo. ¿Cuánto se tendrá que hacer de cada una para que se obtenga una ganancia máxima de 24 centavos?
CorrectoIncorrecto - Pregunta 59 de 61
59. Pregunta
La administración de un hospital analiza el gasto en viáticos de médicos y enfermeras y llega a determinar la función objetivo F(x,y)=12x+7y, así como la región factible que se muestra en la figura, donde los valores se encuentran en cientos de dólares. En su informe, el administrador indica que el punto____es el que minimiza los gastos en viáticos de los médicos y las enfermeras, lo que servirá para planificar las actividades del próximo año.
CorrectoIncorrecto - Pregunta 60 de 61
60. Pregunta
Con base en el caso, complete el enunciado. Una empresa vende X cremas y Y lociones para el cuidado de la piel. Cada producto genera un ingreso de USD 30 y USD 25 respectivamente. La ganancia obtenida por la venta de dichos productos esta determinada por la ecuación G(x,y)= 30x + 25y + 50 y su región factible se muestra en la gráfica, por lo tanto, la empresa debe vender _____ cremas y _____ lociones, para obtener la mejor ganancia.
CorrectoIncorrecto - Pregunta 61 de 61
61. Pregunta
La gráfica muestra la solución de un sistema de desigualdades de un problema de programación lineal, cuya función objetivo es: f(x,y)=30y−20x−10.
CorrectoIncorrecto